If you ever heard of Principal component analysis (PCA), chances are you were intimidated by it at first sight. I was, and I almost had to do it for my thesis. So, PCA and I go way back (not actually, just a year or so really).
To avoid you having to flounder in understanding this concept, I’ll try my best to break down the process in a step-by-step fashion.
First before we get into the nitty gritty, let’s go over some terms that we should address in PCA.
Concepts of PCA
1. What is it?
PCA to simply put it, reduces the number of variables in a set, retaining as much information on the dataset as possible (
magic ). It is a linear transformation technique used to project data onto a new coordinate system, where the greatest variances are in the first coordinates (principal components).
2. What are Principal Components?
Principal components are new variables that are constructed from the linear combinations of the original variables. Below is a real world example I’m using to break the concept down into simpler sections.
Conceptual Example
Imagine you’re a photographer at sporting event. With your camera, you can capture a wide range of details- expressions on the players’ faces, the mood of the crowd, a random dog walker. But, your camera is only limited on what it can capture based on what you can focus on at once. Being the eager artist you are, you want to capture the most important aspects of the scene while maintaining a compelling story.
PCA is like choosing where to point your camera and how much you want to zoom to capture the most significant elements of the scene:
The first principal component is like pointing your camera at a portion of the scene where the action is the most intense. The direction you are pointing captures the most variance or action of the data. This could be Sally Superstar making a triple-play to win the championships.
The second principal component is like adjusting the angle to now capture the next important moment/feature of the scene, which is orthogonal (completely independent) to the first. This new camera direction captures the next most significant variation in the scene, which adds more depth to the story.
Further components would be you changing lenses to capture other details, the dog walker pausing to watch the game, the expression of the coaches and players, weather conditions, etc. Each subsequent component captures progressively smaller variations in the data, providing finer details to the overall picture.
By focusing on just the first few principal components- the winning play, the crowds reaction - you get a comprehensive view of the event without being overwhelmed by the smaller details. Similarly, PCA does this by reducing the dimensionality of the data, by focusing on the most informative aspects, helping you see the bigger picture.
Bringing back the more technical language, the first principal component accounts for the largest possible variance in the dataset. The second principal component provides the next most significant variation in your dataset, with the condition that it is uncorrelated to the first, and so forth.
Now let’s get into the process of actually performing PCA.
The Steps in Running a PCA
The code for the dataset we are using is as follows:
data(iris)
print(head(iris))
Here is a preview:
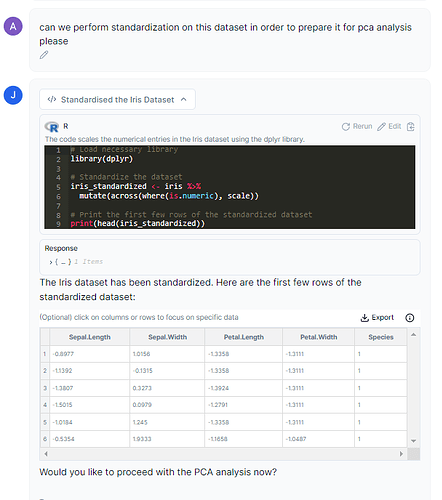
Step 1: Standardization:
This step puts all variables on the same scale, which allows for fair comparisons and combinations of data. Mathematically speaking, this is done by subtracting the mean and then dividing it by the standard deviation for each variable.
Prompt: can we please perform standardization on this dataset in order to prepare it for PCA analysis please?
Step 2: Covariance Matrix Computation:
The purpose of the covariance matrix is to assess how each variable in a dataset deviates from its mean in relation to every other variable. This helps in understanding:
- How much the variables vary (a mouthful) from the mean, and;
- It checks if there is a relationship between the variables (e.g., if two variables are highly correlated, they convey similar information).
Prompt: can we create a covariance matrix on this dataset now please?
For you visual learners:
Step 3: Computing Eigenvectors & Eigenvalues
Eigenvectors and eigenvalues are from the covariance matrix:
- eigenvector tells you the directions the data varies the most.
- eigenvvalues tells you the magnitude of that variance.
For the iris dataset, we can have Julius calculate the eigenvectors and eigenvalues.
Prompt: can we compute the eigenvectors and eigenvalues for this dataset please? Please explain the variance for all the principal components as well please.
We can see that we have a total of four principal components involved in this dataset. To determine which principal components we will retain we can create a scree plot.
Step 4: Creating a scree plot
We can prompt Julius to create a scree plot on the cumulative variance that is explained by each principal component we had it calculate earlier.
Prompt: can we create a scree plot on the cumulative variance of each principal component please?
Looking at the scee plot, we can see that the first two principal components capture about 95.81% of the variance in the dataset. We will keep the first two components as they explain ~95% of the total variance seen in the dataset.
Step 5: Create Loadings and Plotting
Here we will take the original data and plot it into the principal component space using the selected components.
I also like adding in the vectors (loadings), which are the coefficients of the original variables in the principal component space, showing how much each original variable contributes to each principal component.
Step 6: Interpreting PCA Vectors and Relationships
The vectors (loadings) directions and length indicate how much each original variable contribute to the PC. For example, if a vector is pointing in the direction of the PC1, it means that it has a strong influence on the first principal component. Here is a visualization to help understand which section is positive and what section is negative for each PC:
Vector Direction:
- if a vector points towards the positive side of the PC1, it means it is positively correlated with that PC
- if a vector points towards the negative side of the PC1, it means it is negatively correlated with that PC
- If a vector points upwards, it means it is positively correlated with PC2, and if it points downwards, it is negatively correlated
Vector Relationship:
Angles between vectors indicates the relationship between the two:
- If vectors are close to each other (small gap between), that means they are positively correlated
- If vectors are 180 degrees from one another, (opposite directions), it means they are negatively correlated
- If vectors are 90 degrees to one another (perpendicular), it means they are not correlated
Iris Vector Plot
Sepal.Length is located in the negative PC1 and PC2 grid section (top right). It also has a long arrow from the origin (0,0). This indicates that it has a positive correlation. Additionally, it seems to be ~90 degrees from the other vectors, indicating that it does not have much of a relation to those vectors.
Iris Clusters
We can also place circles (ellipses) around data clusters:
If they intersect- as we can see in both Versicolor and Virginica- this suggests that the observations in those clusters are similar to an extent.
The intersection of Versicolor and Virginica clusters with the vectors for petal length, petal width and sepal length indicates that these features have similar values. This means that it would be hard to distinguish between these two species based on these features alone.
Conclusion
Thanks for joining me on this very long guide on PCA analysis. I hope this helps breakdown this very complex topic. As such, happy analyzing!